Современное производство энергии[193]По всему земному шару (точнее, вырабатываемая мощность) составляет около Ю10 кВт. За последние 200 лет производство энергии росло экспоненциально с годовым приростом 3%. Если такой рост будет продолжаться в будущем, то примерно через 300 лет производство энергии достигнет величины Е0= 1014 кВт, т. е. сравняется с потоком энер1ии, поступающей на Землю от Солнца. Так как вся произведенная энергия, в конечном итоге, превращает ся в тепло, то это приведет к нарушению теплового баланса планеты и, как следствие, к ее перегреву со всеми вытекающими отсюда последствиями (таяние льдов, повышение уровня Мирового океана и т. д.). Для того чтобы этого не произошло, производство энергии должно быть 01раничен0, оно не может превышать предельно- то значения, составляющего определенную долю от величины Е(). Обычно считается, что предельное значение составляет 1% от полной энер] ии, поступающей на Землю от Солнца. Более осторожная оценка составляет 0,1%. Соответствующие предельные значения производимой энер! ии: £] = 10п кВт и £2=Ю12 кВт. Назовем их первым и вторым тепловым пределом. Пепвый предел при темпах роста 3% в год будет достигнут через 77 лет, а второй — через 153 года. После дост ижения предела производство энергии должно бы ть стабилизировано па этом уровне.
Хватит ли энергетических ресурсов для достижения этих пределов? В настоящее время основным источником вырабатываемой энергии является химическое топливо: уголь, нефть, газ. По дан ным экспертов «Римского клуба»[194] запасы нефти и газа (с учетом пока еще не разведанных месторождений) истощатся к 2020 г., а запасов угля хватит на весь XXI век. Согласно В. С. Троицкому[195], с учетом вероятных запасов топлива, энергопроизводство может расти с современным темпом вплоть до первого теплового предела; если затем оно будет стабилизировано на этом уровне, то запасов топлива всех видов (включая уран для атомных электростанций) хватит еще на 130 лет. Это время можно значительно продлить, если к момен ту истощения ресурсов будет освоена термоядерная энергия. При постоянном производстве энергии на уровне теплового преде та запасов водорода в Мировом океане (термоядерного горючего) хватит на сотни миллионов лег.
Другим практически неисчерпаемьгм источником является солнечная энергия. Очевидно, что использование этой энергии не приводит к нарушению теплового баланса, так как часть радиации, изымаемой энергетическими установками из солнечного потока, после переработки вновь превращается в тепло. При этом предполагает ся, что энергетические установки располагаются только на поверхности Земли. (Если расположить их в межпланетном пространстве, а затем ^экспортировать энергию на Землю по каналам СВЧ или другим способом, то это создаст дополнительный поток энергии на Землю и вновь приведет к эффекту перегрева.) Размещение солнечных энергетических установок на Земле, хотя и не нарушает ба ланса, тем не менее, тоже приводит к ограничениям в производстве энергии, ‘ли покрыть такими установками 1% площади Земли, то при преобразовании солнечной энерг ии в электрическую с КПД 10% общее количество вырабатываемой энергии составит 10-3 £„, т. е. будет на уровне первого теплового предела Е = 10’1 кВт. При покрытии 10% плогцади Земли производство энергии будет на уровне второго теплового предела Е2 = 1012 кВт. Дальнейшее наращивание энергетических установок иск игочаег из нормального использования слишком большой процент площади Земли. Кроме того, это может привести к перераспределению энер! ии на планете и вызовет нежелательные изменения климата. Таким образом, при использовании солнечной энергии мьг, фактически, сталкиваемся с теми же пределами.
Подчеркнем еще раз, что ограничение производства энерг ии не связано с недостачей энергетических ресурсов, а вытекает из необходимости сохранить глобальное равновесие природных процессов на Земле. В этом коренное отличие проблемы перег рева от про блемьг истощения недр Земли. Хотя обе они приводят к необходимости ограничить безудержный рост производства на земном шаре. Рассмотрим теперь рост народонаселения на Земле.
5.2.3. Рост народонаселения. Довольно очевидно, что абсолкн — ньгй прирост населения должен бьгть пропорционален численное ти населения. Если взятг какой-то однородный в демографическом отношении регион, то из двух пунктов этого региона прирост будет выше там, где больше численность населения. Точно так же, чем больше численность населения в неко горый момент времени чем больше и прирост населения в этот момент. Статистика показывает, что абсолютный прирост (IN за небольшое время Dt равен
DN = aN dt. (5 6)
Внешне это выражение напоминает экспоненциальный закон (5.2), но надо иметь в виду, что экспонента получается из него только при условии а. = const. Относительный прирост населения а зависит от целого ряда фак. оров: биологических, географических, исторических, социально-экономических. Поскольку эти факторы, во всяком случае некоторые из них, меняются с течением времени, относительный прирост населения, вообще говоря, есть функция времени: а = а(г). Поэтому и закон роста народонаселения может отличаться от экспоненциального.
Как реально растет народонаселение па Земле, что i оворят стати стические данные? Согласно оценкам специалистов286, в очень дав ние времена — от 1 ООО ООО до 6000 лет до нашей эры — числен ность населения практически не менялась со временем, составляя 2 + 5 млн человек. Начиная примерно с 6000 г. дон. э. отмечается рост народонаселения. В период с 6000 по 3000 г. до н. э. численность населения составляла 5 + 20 млн чел., с 3000 по 2000 к. до п. э. — 20 40 млн чел., с 1000 г. до н. э. по 250 г. н. э. — 100 + 200 млн чел. и с 250 по 1500 г. н. э. — 300 + 400 млн человек. Конечно, эти оценки весьма приблизительные. Согласно справочнику Урланиса287, население мира составляло:
|
Год (и. э.) |
1000 |
1500 |
1650 |
1750 |
1800 |
1850 |
1900 |
|
Население млн чел. |
288 |
436 |
545 |
728 |
911 |
1181 |
1617 |
Более поздние данные можно найти в Статистических ежегод никах ООН288.
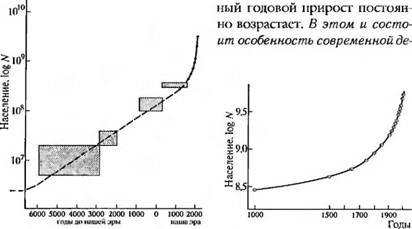
На рис 5.2.1 показано, как менялась численность населения Зем ли за период от 6000 г. до н. э. по настоящее время. По горизон-
ГтЛада И В., Писаржееский О Н Контуры крадущего — М.: Знание, 1965 С. 31.
"’Население мира / Под ред 1>. Ц Урланиса. — М.: Политиздат, 1965 С. 8. 2**Unitcd Natron? Statistical Yea. book
Тальмой оси отложено время /, по вертикальной — численность населения в логарифмическом масштабе (log N). Если бы население росло экспоненциально, то на этом графике мы должны были бы получить прям) ю линию В действительности линия, выражающая рост народонаселения со временем, начиная приблизительно со средины второго тысячелетия, заметно отклоняется от прямой, при чем она уходи г вверх все круче и круче. Колее детально это видно на
Рис. 5 2 2 Значит, относитель-
|
Рис. 5.2 1. Численность населения па земном шаре, согласно оценкам [286 287] По горизонтальной оси отложено время в годах, по вертикальной числеиност ь населения в логарифмическом масштабе (log N) |
Рис. 5.2.2. Роет численности населения па Земле [28 7 288].
По горизонт альной оси годы, по вертикальной — численность иасслсния в логарифмическом масштабе (log N)
Мографической ситуации: она характеризуется не только увеличением абсолютной численности населения N, но и возрастанием среднегодовых темпов роста — возрастанием относительного при роста населения а. Как быстро возрастает прирост населения’1
В 1960 г. в журнале «Science» была опубликована статья трех авторов X. Форстера, П. Мора и J1 Эмиота, которая называлась «День Страшного суда: пятница, 13 ноября 2026 года»[196] . Используя тщательно отобранные статистические данные, авторы показа
ГЛАВА 5 Эволюцш. космических цивилизаций 472 ——— ~
Ли, что относительный прирост населения растет так же быстро, как само население, т. е.
TOC o "1-3" h z сс(/) = agW(/). (5.7)
Подставляя это выражение а в (5.6), найдем:
DN = a0[N(t)]2dt. (5.8)
Чем объясняется такая зависимость, остается неясным. Выражению (5.8) соответствует следующий закон роста народонаселения:
N(T)= ~ ~г~ г — (5.9)
<*„(/.-о
Нетрудно узнать в этом выражении уравнение гиперболы.
Следовательно, численность народонаселения изменяется по гиперболическому закону. При 1 — U N(T) = т. е. население Земли должно достичь бесконечности! Когда наступит этот роковой момент? Неожиданный результат состоит в том, что он совсем «не за горами». Coi ласно вычислениям авторов, это должно произойти в 2026 г., точнее = 2026,87 ± 5 ,5, если T отчитывается от начала новой эры.
Если величина определена, можно, откладывая по оси абсцисс значения log(f„- /), а по оси ординат значения log N, построить график зависимости (5.9) в виде прямой линии с отрицательным наклоном (-1) При T —¥ Tt (/»- T) —¥ 0, и прямая линия устремляется в бесконечность.
Момент /„ на графике определить невозможно, ибо при T — Tt
LOg(/,-0 = -ос.
И. С. Шкловский29′ ташел убедительный способ наглядно про демонстрировать справедливость гиперболического закона, не зная зеличины /*. Обозначим величину 1 /N через у, тогда вьгражение (5.9) можно переписать в виде
Y = a0(t„-t). (5.10)
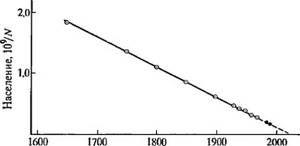
А это есть уравнение прямой. Следовательно, если мьг построим ■ рафик, на котором по горизонтальной оси отложит время /, а по вертикальной — величину у = 1//V, то мьг должны получить пря
2,0 Шкловский И. С Зселеиная, жизнь, разум. — М; Наука, 1965.
Мую линию. Рис. 5.2.3 иллюстрирует сказанное. Мы действительно получаем прямую линию причем статистические данные (точки на Iрафике) очень хорошо, почти без всякого отклонения, ложатся на эту прямую. При T = = 0. Следовательно, прямая пересекает ось абсцисс в точке, соответствующей T = T*. Таким образом, можно I рубо оценить этот момент прямо по графику как точку пересечения прямой линии с осью абсцисс, а более точно можно вычислить этот момент, например, методом наименьших квадратов. Для пря-
|
Годы Рис. 5.2.3. Гиперболический рост народонаселения, по И. С Шкловскому. По горизонтальной оси — время в годах от начала новой эры, по вертикальной — обратная величина численности населения 10WV |
Мой, изображенной на рис. 5.2.3, критический момент соответствует 2028 г.
Итак, в настоящее время население Земли растет по гиперболическому закону. Но каковы границы его применимости?
Согласно С П. Капице[197], экстраполяция гиперболического закона в прошлое показывает, что он удовлетворительно согласуется с оценками численности населения на интервале времени порядка одного миллиона лет. Однако дальнейшая экстраполяция в прошлое приводит к неправдоподобным и даже абсурдным результатам так, согласно гиперболическому закону, в момент возникновения физической Вселенной (около 20 млрд лет назад) на Земле уже жило 10 человек; а время возникновения первого человека (N = 1) Уходит в прошлое на 200 млрд лет, т. е. задолго до возникновения
ГЛАВА S Эволюция космических цивилизаций 474_____ _ ____
Земли, Солнечной системы и Метагалактики Ясно, что гипербо лический закон нельзя экстраполировать слишком далеко в прошлое.
С другой стороны, если бы гиперболический закон был сира ведлив вплоть до рокового момента T = /„, это бы означало, что численность населения за конечный промежуток времени увеличивается до бесконечности. Очевидно, это невозможно, ибо требует бесконечно быстрого прироста населения. Между тем годовой прирост не может быть бесконечным, он ограничен естест венными биологическими причинами (фертильноегь не может быть бесконечной!), не говоря уже об экономических н социо культурных факторах. Отсюда следует, что гиперболический закон нельзя экстраполировать до значений, сколь угодно близких к При некотором значении / < /* гиперболический закон роста теряет силу и Должен смениться новым демографические законом. Атак как значение Lt близко к современному моменту, то смена демографического закона должна произойти в самое ближайшее время (а возможно, уже происходит).
На рис. 5.2.3 прямая линия построена по данным о численнос ти народонаселения до 1970 г., эти данные изображены па рисунке кружками, темные точки изображаю i более поздние данные, относящиеся к 1987 и 1991 гг. Как видно, вплоть до начала 1990 х годов гиперболический закон все еще сохранял силу. Это связано с влиянием развивающегося мира. Для развитых стран мира прирост населения прошел через максимум и начал замедляться в середине XX века*92. Но динамика роста населения Земли определяется развивающимися странами, а здесь прирост населения до последнего времени, видимо, все еще продолжал расти. Тем не менее ясно, что в ближайшее время ситуация должна измениться, и отклонение от гиперболического закона для всего населения Земли станетощу гимым.
Какой закон должен прийти на смену гиперболическому? Смена закона может произойти либо вследствие катастрофы из-за слиш ком быстрого нарастания процесса, либо в результате плавного изменения характера роста. Рассмотрим последний, более благоприятный случай.
Поскольку годовой прирост определяется разностью между рож даемосгыо и смертностью, его возрастание можег происходить либо за счет сокращения смертности, либо за счет увеличения рождаемости (либо гго обеим причинам вместе). В последние ci о лет ия ос-
2,2 Капица С П. Цит раб Новную роль, по-видимому, играло сокращение смертности, вследствие успехов медицины, санитарно-эпидемических и других мероприятий Сокращение смерт ности, в целом, по всему земному шару перекрывает уменьшение рождаемости в «цельных (особенно в развитых) странах, так что естественный прирост населения на Земле возоастает со временем Менее ясно, почему он раст ет столь же ст ремительно, как само население, что собственно и приводит к гиперболическому закону. Это пока остается 3ai адкой. Тем не менее можно заключи ть, что в пределе, когда смертность достигнет минимальной величины (например, смертность от болезней и несчастных случаев в детском и производящем возрасте будет пренебрежимо мала), а рождаемость установится на некотором оптимальном уровне, определяемом совокупностью биологических, экономических и социо культурных факторов, —дальнейшее увеличение годового прироста прекратится, и население будет расти при постоянном годовом приросте, т. е. экспоненциально.
Эспоненциальное развитие также приводит г. бесконечной численности населения, но, в отличие от гиперболического роста, пе на конечном, а на бесконечно длительном интервале времени. Практическое значение имеет вопрос о том, как скоро при экспоненциальном росте население Земли достигнет критической плотности. Последняя не обязательно зависит от истощения ресурсов, но может определят ься социально-психологическими и иными факторами
Переход к экспоненциальному росту представляется наиболее естественным, ибо не требует никаких рейдирующих воздействий. Однако это не единственный и, возможно, вообще переали (усмый вариант. Существует ряд прогнозов численности населения Земли, в том числе официальные прогнозы ООН[198]. Они дают достаточно разнообразный спектр возможностей, включая неограниченный рост и деградацию (уменьшение численности населения), начиная примерно с середины XXI века. Наибольший интерес представляет упомянутая выше модель С. П. Капицы, которая приводит к стаби лизации населения.
С П. Капице, по-видимому, впервые удалось описать закономерности роста народонаселения Земли на огромном промежутке времени от «происхождения человека» до наших дней, Длительность этого периода по данным современной антропологии около 4,5 млн лет. С П. Капица разделяет его на три эпохи, Ранняя эпоха А, когда население росло очень медленно, изменяясь от нуля пропорционально ctg /; основная эпоха В, когда имеет место гиперболический закон роста, при котором относительный прирост населения а непрерывно увеличивается; и поздняя эпоха С, для которой начинает сказываться ограничение на относительный прирост а С. П. Капица показал, — по изменение численности население во все три эпохи может быть описано одной общей формулой и определил временные границы перехода от одной эпохи к фугой Эпоха А на чинается около 4,4 млн лет тому назад и длится 2,8 млн лет, около 1,6 млн лет тому назад она сменяется эпохой В, длящейся почти до современного момента, она охватывает палеолит, неолит и весь известный историчес кий период развития человечества. Переход к эпохе С падает на последние десятилетия XX века В эту эпоху население растет пропорционально arcctg [(/*-/)/т]. При T —> оо численность населения стремитсу к некоему предельному значению Nup. Для различных параметров модели Nllp Равняется от 10 до 25 млрд чел.
Модель Капицы дает весьма оптимистический сценарий разрешения демографической ситуации на Земле. Однако имея в виду, что пока еще переход к стабилизации для всего земного шара не заметен, мы рассмотрим менее благоприятную ситуацию, когда после смены гиперболического закона некоторое время продолжает дей ствовать экспоненциальный закон роста. Как скоро в этом случае мы столкнемся с положением, когда вступят в силу ограничения, препятствующие дальнейшему экспоненциальному росту?
Выше мы видели, что производство энергии на земном шаре ограничено некоторой предельной величиной Епр, связанной с «эф фектом перег рева». После достижения этого предела энергетика должна быть стабилизирована. Если население будет продолжать расти экспоненциально, то производство энергии на душу населения будет экспоненциально уменьшаться. Чтобы этого не произошло, численность населения также должна быть стабилизирована. Если мы хотим обеспечить производство энергии на душу населения, по край ней мере, не ниже современного, то численность населения не должна превышать величины Nnp = £(ф/е0, где е0 — современное производство энергии на душу населения. Поскольку Еар заключено между Еу и Е2, то /Vlip заключено между Nt и N2, где /V] = Е^/г0, N2 = £2/е0. Принимая е0 = 2 кВг/чел., Ех = 10й кВт, Е2 = 1012 кВт, получим /V] = 50 млрд чел., N2 = 500 млрд чел. Эти величины можно назвать, соответственно, первым и вторым энергетическим пределом для населения.
Сможет ли Земля прокормить такое население? Фон Хорнер при — води^ такой расчет — 1 км2 суши, засеянной пшеницей (или другой столь же продуктивной куш гурой), при урожае 30 центнеров с одного гектара дает 11 ■ 108 калорий в год 11 лребноегь человека составляет в среднем 9 -105 кал/год. Следовательно, 1 км2 суши может про кормить 1200 человек. Если предположить, wo вся поверхность суши превращена в культурную пашню, то она сможет обеспечить пищей 180 млрд чел. Эта величина находится как раз между первым и вторым энергетическим пределом для населения.
Помимо энергетического и пищевого, существует территориальный предел Он связан с предельной плотностью населения. В настоящее время средняя плотность населения на земном шаре состав тяет 36 человек на 1 км2 суши. В крупных городах, таких, как Москва, плотность населения около 10 тыс. чел. на 1 км2, это примерно на порядок выше плотности, соответствующей пищевому пределу. Если бы средняя плотность населения на Земле соответствовала этой величине, вероятно, нормальное функционирование цивилизации было бы невозможно. В. С. Троицкий принимает предельную плотность 50 чел. на 1 км2 земной поверхности (считая сушу и море). Это дает предельную численность населения на Земле 25 млрд чел. Трудно сказать, является ли принятая плотность допустимой.
Фон Хорнер обращает внимание на «эффект перенаселения», связанный с чрезмерно большой плотностью Он ссылается на исследование П. Лейхаузеиа и других ученых, занимающихся изучением поведения животных. Эти исследования показали, что недостаток жизненного пространства приводит к существенному изменению поведения животных, к полному развалу их социальной структуры и образа жизни (взрослые особи перестают заботиться о детенышах, развиваются агрессивность, страх, злобность). Причем это вызвано ие недостатком пнщи, а именно недостатком пространства. Недостаток пространства приводит к страданиям, которые не связаны с прямой угрозой от близкого соседства с сильными животными. Слабые животные страдают от перенаселения даже в том случае, когда они полностью защищены от них ширмами. Причем их страдания могут доходить до такой степени, что вызывают полное изменение характера и даже смерть. Для социальных животных, которые не могут жить в полном одиночестве, существует определенная оптимальная плотность. При превышении ее они могут адаптироваться к новым условиям, но только до тех пор, пока плотность не достигнет некоторой предельной величины, за которой разрушаются все социальные порядки и возобладает «неконтролируемая агрессивность». Лейхаузен называет этот предел «пределом терпимости*. В определенной мере все ска 1анное относится и к человеку (вероятно, в той мере, в какой на поведении человека сказывается его животная природа) Об этом свидетельствует роет преступности в крупных городах и другие социальные феномены. По мнению фон Хорнера, большая часть наших политических и социальных проблем связана именно с перенаселением, По видимому, у человека существует врожденный «предел терпимости», как часть нашего гепетического наследства. Противоречие, связанное с перенаселением, состоит в том, что человек для своей социальной жизни нуждается в больших городах, как центрах промышленности, торговли, науки и культуры. В то же время ссучивание людей в них приводит к перенаселению. Очень важно установить, какова оптимальная плотность и «предел терпимости» для человечества. Фон Хорнер полагает, что мы уже прошли этот предел
Как быс гро дос гигаюгея другие пределы, о которых говорилось выше? Это зависит от темпов роста народонаселения в будущем, а они определяются моментом, когда гиперболический закон роста сменится на экспоненциальный — Пусть это произойдет в момент Tc При значении годового прироста ас; тогда, начиная с этого момен та, рост народонаселения будет определяться выражением
N{t) = N(tc)e^u •>. (5.11)
На самом деле между гипербо [ическим и экспоненциальным законом должен существовать некий промежуточный переходный закон, когда а(/) растет вместе с /, по не столь быстро, как N(t). Однако для грубых оценок можно считать, что гиперболический закон пере ходит непосредственно в экспоненциальный при T = Tc. Выше мы отмечали, чго гиперболический закон сохраняет силу вплоть до начала 1990-х годов Предположим, что «переход на экспоненту» произойдет в последнем десятилетии XX века. Примем для определенности, что момент /с соответствует 1995 г. Тогда N(tc) = 6,2 млрд чел., ас = 0,03 С этими параметрами первый энергетический предел /V] = 50 млрд чел. будет достш нут через 70 лет. Второй энергетический предел N2 = 500 млрд чел. — через 146 лет; пищевой предел 180 млпд чел. — через 112 лет и территориальный предел Троицкого 25 млрд чел. — через 46 лет.
Внимательный читатель, наверное, заметил, что время достижения энергетичеекчх пределов, тпя населения Nx и N2 практически совпадает е временем достижения теплового предела для энергетики Ех и Ег. Это понятно, ибо для принятого нами момента перехода от гиперболического закона к экспоненциальному годовой прирост населения ас составля ег 3%, как и прирост производства энергии, тоже равный 3%. Если смена демографического закона произойдет позже, то прирост населения будет выше 3%, и все названные пределы будут достигнуты раньте.
Вывод о том, что при экспоненциальном росте населения рано или поздно будут достигнуты предельные значения, является тривиальным. Поучительным и несколько неожиданным обстоятельством является то, что эти критические значения достигаются в срав нительно недалеком будущем. Учитывая современное очень неустойчивое состояние мира, сомнительно, чтобы за остающийся короткий промежуток времени могли быть выработаны необходимые регу лирующие механизмы. Не следует. акже забь. вать, что мы рассматривали благоприятный вариант смены демографического закона. Но нельзя исключить, что до «рокового дня» 1 иперболический рост народонаселения не успеет плавно смениться другим зако ном, и тогда человечество столкнется с очень тяжелой кризисной ситуацией.
Возникает вопрос: нельзя ли решить. пу проблему за счет расселения человечества в космическом пространстве? В начале 1970 — х годов в США группой инженеров и физиков из Принстона пол руководством О’Нейла был представлен тщательно разработанный проект сооружения поселений для расселения людей в межпланетном пространстве На первой ста дин проекта предусматривается сооружение станции на 10 тысяч человек, стоимость ее оценивается в 100 млрд долларов, срок сооружения 10-20 лет. Если начать реализацию проекта немедленно, он может быть завершен во втором десятилетии XXI века, по пока этот проект еще находится па рассмотрении в НАСА. Следующая оадия проекта предусматривает сооружение гораздо более крупных поселений на 40-50 млн чел, и для ее осуществления потребуются уже многие десятилетия. Это, действительно, впечатляющий, грандиозный проект1 По существу, он пред сывляет собой проектное воплощение мечты К. Э. Циолковского о создании «эфирных городов» в межпланетном пространстве Реализация этого проекта позволила бы практически прис гупитп к расселению че ловечества за пределами Земли. Но надо ясно представлять, что это не решает проблемы народонаселения на земном шаре
Действительно, уже к середине 1990-х годов абсолютный прирост населения составил около 180 млн чел. в год или около 500 тысяч чело век в день. Именно такое количество людей (полмиллиона человек!) пало Ежедневно расселять в космическом пространстве, если мы хотим решить проблему народонаселения за счет Космоса Таким образом, одна или несколько станций первой очереди, даже если они будут построены в начале XXI века, не решат проблемы А к моменту сооружения косми ческих поселений торой очереди с населением 40-50 млн чел. ежегод ный прирост населения на Земле может превысить 1 млрд человек. Все это говорит о том, что проблему народонаселения, как совершенно спра ведливо подчеркивает фон Хорнер, надо решать здесь, на Земле (не путем 6ei ства) и очень скоро. Столь скоро, что резерва времени у нас, по существу, уже нет