При начале периода деятельности, говорит Гайная Доктрина, в силу повиновения вечному и непреложному закону, совершается распространение этой Божественной Сущности… и феноменальный или видимый мир является конечным результатом длинной цепи космических сил, последовательно приведенных в движение. Так же, ко» да наступает возвращение к пассивному состоянию, происходит сокращение Божественной Сущност и, н предыдущее созидание постепенно н последовательно растворяется. Видимый мир разлагается, его материя рассеиваете,,, и единая «Тьма», еще раз одинокая, лежи! над лнком «Бездны»
Е. П. Блаватская
Расширение Вселенной было открыто Э. Хабб. юм в 1929 г. по наблюдениям с 2,5-метровым телескопом обсерватории Маунт Вил-
сон. Это открытие основано на результатах измерения лучевых скоростей га 1актик. Лучевой скоростью называется состав гяющая полной скорости, направленная вдоль луча зрения наблюдателя. Она определяется по доплеровскому смещению спектральных линий. Если галактика удаляется от нас, все линии в ее спектре смещены в сторону красного конца, т. е. длины волн их возрастают; если галактика приближается к нам, линии смещаются " фиолетовому концу, длины волн их убывают. Величина смещения ДА, зависит от лучевой скорост и галактики Vr. Если эта скорость много меньше скорости све та, то
Здесь с — скорость света, Апабл— наблюдаемая длина волны, А — лабораторная длина волны, т. е. длина волны линии в случае неподвижного источника. Зная из наблюдений величину ДА., можно определить лучевую скорос гь Vr.
Первые измерения лучевых скоростей галактик были выполнены В. Слайфером на Ловелловской обсерватории в самом начале XX века. Уже эти измерения показали, что галактики обладают колоссальными скоростями в несколько сотен километров в секунду, во много раз превосходящими скорости звезд. Причем подавляющая часть галактик имеет положительные лучевые скорости Это могло означать, что Солнце дви жется относительно наблюдаемой системы галактик со скоростью в несколько сотен км/с, или рой галактик удаляется от Солнца с той же, но противоположно направленной скоростью. Так как каждая галактика роя имеет еще свою собственную скорость, то наблюдаемая скорость галактики складывается из скорости удаления всего роя н скорости движения каждой галактики внутри роя Чтобы разобраться в картине дви жения, надо было иметь лучевые скорости для большого числа галактик. Слайферу, с его 60 сантиметр» Ibmm телескопом, эта задача была непосильна, он мог измерять лучевые скорости только самых близких галактик.
|
|
В конце 1920-х годов в измерение лучевых скоростей галактик включилась Маунт Вилсоновская обсерватория. Спектры галакт ик на 2,5-метровом телескопе получал М Хьюмасон, а расстояния до них по наблюдениям на том же телескопе определял Хаббл. В 1929 i., накопив достаточный наблюдательный материал, Хаббл сопоставил данные о лучевых скоростях галактик с расстояниями до этих галактик Оказалось, что скорость удаления галактик пропорциональна
расстояниям до них (рис. 2.2.1). Чем дальше расположена галактика, тем с большей скоростью она удаляется от Солнца:
Vr = H-r. (2.2)
Эту зависимость, в честь ее первооткрывателя, стали называть законом Хаббла, а коэффициент пропорциональности — постоянной Хаббла (Hubble), которую стали обозначать буквой Н. Это одна из
«.1000 2 и:
I500 §-
|
|
|
S^co 0 |
|
1 |
Б о
Расстояние, Мпк
Рис. 2.2.1. Зависимость между лучевой скоростью галактик и расстоянием до иих, полученная Э Хабблом
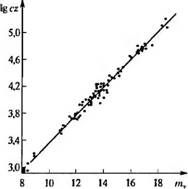
Рис. 2.2.2. Зависимость между красным смещением и видимой звездной величиной галактик (закон Хаббла).
По данным Сендиджа и Таммана, 1981 г. черный прямоугольник в левом нижнем углу соответствует области данных, доступных Хабблу в 1929 г.
Фундаментальных космологических постоянных. В настоящее время закон ХабЬла проверен по огромному числу удаленных галактик и квазаров (рис. 2.2.2). Справедливости его подтверждается наблю дениями в разных диапазонах волн от радиодиапазона до рентгеновского.
Закон Хаббта означает, что вся наблюдаемая система галактик расширяется. На первый взгляд, может показаться, что, поскольку все галакти. ш удаляют ся от Солнца, — наша Галактика, вместе с Солнцем, расположена в центре этого расширяющегося роя. Но на самом деле это не так. Если две галактики удаляются от третьей со скоростями, пропорциональными расстояниям до этой галактики, то и скооость их взаимного удаления также пропорциональна расстоянию между ними[87]. Поэтому наблюдатель, в какой бы га гакти-
ке он ни находился, будет видеть, что другие галактики разбе1 аются от него со скоростями, пропорциональными расстояниям до этих j алактик. Вся система галактик напоминает разлетающийся из улья пчелиный рой, или расширяющееся облако газа. В одной популярной книге я прочел сравнение с пирогом, нашпигованным изюмом: когда пирог печется, он поднимается, расстояние между изюминками зозрасгает. Можно преде / акт ь ссбс также резиновый шар с металлическими заклепками, укрепленными на его поверхности; если надувать шар, поверхность его расширяется и расстояние между заклепками увеличивае тся.
Расширение Вселенной характеризуется величиной красного смещения:
Z=K:,(,~K„, _ (2.3)
Rut
При малых Z — ко1да скорость расширения мала по сравнению со скоростью света, справедливо соотношение V = Cz, совпадающее с формулой (2.1). В этом случае, в соответствии с законом Хаббла, имеется линейная зависимость между г и г. На больших расстояниях, когда скорость расширения становится сравнимой со скоростыо света, соотношение V = сх не выполняется и, соответственно, зависимость между красным смещением и расстоянием отклоняется от линейной. В этом случае надо пользоваться формулами теории относительности124, из которых следует, что при V = с Z = Таким об разом, Z может принимать любые значения от 0 до Максимальное значение z, которое исполгзолал Хаббл в 1929 г., сосгавля ло 0,004, в настоящее время наблюдакпея квазары, для которых г > 5. Чем больше z, тем дальше от нас находится наблюдаемый объект, тем дальше в прошлое отстоит момент излучения наблюдаемого нами света. Таким образом, красное смещение характеризует как распределение объектов в пространстве в заданный момент времени, так и распределение их во времени, т. е. позволяет проследить историю Вселенной.
Несмотря на необычность результата, полученного Хабблом, он не был полностью неожиданным: предсказание о расширении Вселенной вытекало из космологических моделей, построенных на основе общей теории относительности А. Эйнштейна.
12,1 При не очень сильных полях тяготения можно пользоваться формулой снеци-
Альнои теории относительности г +1 = Л————— — .
Первую космологическую модель, опирающуюся на ОТО, построил сам Эйнштейн в I917R. Исходя из господствовавших в то время представлений о неизменности Вселенной, Эйнштейн искал стационарное решение, в котором расстояние между любыми двумя точками в пространстве и другие параметры Вселенной не меняются со временем. Однако уравнения общей теории относительности не давали такого реше ния Чтобы избежатт этой «неприятности», Эйнштейн ввел в свои уравнения дополнительную величину А-член (лямбда-член), который описывает действ} ющие во Вселенной гипотетические силы отталкивания Подобно силам гравитации, эти космологические силы отталкивания носят универсальный характер, т. е. они ие зависят от свойств гел, а зависят только от их взаимного расстояния. Но в отличие от сил гравитации они не убывают, а, напротив, возрастают с расстоянием, увеличиваясь пропорционально г. В обычных масштабах, с которыми мы имеем дело, и даже в астрономических масштабах вплоть до размеров Галактики, эти силы совершенно ничтожны по сравнению с силами гравитации, и их можно не учитывать. Но на космологических расстояниях силы отталкивания становятся сравнимыми с силами тяготения. Взаимодействие этих двух противоборствующих сил и определяет динамику Вселенной. При определенных условиях, при определенном расстоянии г, обе силы уравновешивают друг друга, и Вселенная остается стационарной. Именно такую модель Вселенной и построты Эйнштейн.
Мир Эйнштейна оказался стационарным, но при этом он обладал необычными геометрическими свойствами. Будучи бе граничным (мы могли бы двигаться в этом мире в любом направлении сколь угодно долго и никогда не вышли бы за его предел), он имеет конечный объем. Геометрия Евклида в этом мире неприменима, здесь действует геометрия Рима — па. Это замкнутый мир — мир постоянной положительной кривизны. Аналогом такого трехмерного мира среди двумерных многообразий мо жет служить поверхность сферы. Она замкнута и безгранична; двшаясь вдоль се поверхности, двумерное существо никогда не выйдет за ее пределы Между тем поверхность сферы конечна, она равна 4л/?2. Радиус сферы R определяет постоянную положительную кривизну (к = 1 /R2) в каждой ее точке. Геометрия на сфере (сферическая геометрия), как известно, отличается от евклидовой геометрии, действующей на плоской поверхности. Подобно тому как на сфере, двигаясь по большом}’ кругу, можно обойти сферу и прийти в исходную гочку — так же и в трехмерном замкнутом мире, двигаясь по геодезической линии125, мы, в конце концов, обойдем этот мир и вернемся к точке старта.
Принципиальным недостатком модели Эйнштейна, как было обнару жено позже, является ее неустойчивость — малейшее изменение парамет ров приводит к тому, что Вселенная выходит из равновесия и больше не возвращается в это состояние Подобные системы не могут реализовать ся в Природе. В дальнейшем Эйнштейн сам отказался от своей модели и даже считал ее самой большой ошибкой в своей жизни. Но введенные
125 Геодезическая линия есть обобщение понятия прямой на случай неевклидовой 1 еометрии, она играет ту же роль, что н прямая в евклидовом пространстве В частности, дуга гсо (езнческой линии, подобно отрезку прямой, определяет кратчайшее расстояние между двумя точками им космологические силы отталкивания сыграли очень ьажную роль в космологии, хотя значение их не сразу было оценено.
Силы отталкивания не зависят от плотности вещества во Вселенной. Они будут действовать н при отсутствии вещества — в вакууме. Поэтому нх назчвают еще силами гравитационного отталкивания вакуума Модель Вселенной, в которой, плотность вещества ничтожно мала — гак называемая щустая» модель была рассмотрена голландским астрономом В де Ситгером сразу после появления модели Эйнштейна, в том же 1917 г. В «пустой» Вселенной действуют только силы отталкивания >’си лами тяготения вещества можно пренебречь), поэтому такая Вселенная будет расширяться. Причем поскольку силы отталкивания пропорциональны расстоянию, то и скорость взаимною удаления частиц вещества в «пустой» Вселенной (а под такими частицами можно подразумевать целые галактики) будет пропорциональна расстоянию Это и есть закон Хаббла Модель де Ситтера, в силу’ присущих ей «экзотических» свойств (на которых мы пока останавливаться не будем) практически не использовалась в космологии И только спустя много десятилетий выяснилось, что с ее помощью можно описать самые раиние этапы развития Вселенной
Задача об эволюции Вселенной в общем виде — без априорных предположений о ее стационарности или об отсутст зии вещества — была решена советским математиком А. А. Фридманом в 1922 г. Единственное условие, которое Фридман положил в основу своей теории, это предположение об однородности и изотропии Вселенной. Однородность означает равномерное распределение вещества во Вселенной в больших масштабах. Как мы видели в предыдущем параграфе, это предположение подтверждается астрономическими наблюдениями. Изотропия утверждает равноценность всех напрар."сний в пространстве. Оба предположения кажу тся вполне естественными (самыми простыми) и в дальнейшем они полностью подтвердились. Основной вывод, который вытекает из полученного Фрид маном решения космологичесглх уравнений, состоит в следующем: материя во Вселенной в больших масштабах не может находиться в покое. Вселенная в целом яв-ьяется нестационарной, она может либо расширяться, либо сжиматься[88].
Пабота Фридмана имела выдающееся значение. Эйнштейн не сразу согласится с Фридманом, но загем дал высокую оценку его работе, отметиЕ фундаментальную важность теоретического вывода о нестационарности Вселенной[89]. А. А. Фрчдман умер в 1925 г., не дожив всего несколько лет до триумфа своей теории. Несмотря на признание и высокую оиенку Эйнштейна, его работа на многие годы выпала из поля зрения не только астрономов, но и физию >в теоретиков.
В 1927 г. аббат Ж. Леметр, бельгийский астроном (ученик Эд — цингтона), независимо от Фридмана получил решение космолот и — ческих уравнений и подтверди;! вывод о нестационарности Вселен ной. Таким образом, к концу 1920 х годов в космологии были получены очень важные результаты, касающиеся эволюции Вселенной. Тем не менее они не привлекли внимание астрономов. Анализируя это обстоятельство, А. С. Шаров и И Д. Новиков отмечают, что одна из причин состояла в сложности теории и разобщенности меж ду теоретиками л наблюдателями. Другал причина, по их мнению, — «психологическая, вероятно, состояла в необычности выводов теории, утверждавшей, например, возможность замкнутости пространства или существование начала эволюции нашею мира в прошлом. Астрономам-практикам, с помощью новых телескопов проникавшим все дальше и дальше в глубины пространства, психологически было трудно поверить в реальность таких утверждений, в корне менявших их представление о Вселенной»[90]. Вот почему такое большое значение имеет работа X 1ббла, экспериментально подтвердившая факт расширения Вселенной. Это открытие, несомненно, является крупнейшим достижением сстсствознаниг XX века.
Необходимо отметить, что расширение Вселенной никак не влияет на отдельные тела: расстояние между галактиками увеличивается, но размеры самих i «тактик (а тем более звезд и планет) остают ся без изменения — подобно тому, как не меняются размеры пчел в разлетающемся рое или размеры молекул в расширяющемся облаке газа. То есть гравитаг ионно связанные тела в расширяющейся Вселенной не подвержены космологическому расширению.
Каждая галактика участвует в общем космологическом расширеиии и имеет, кроме того, свое собственное движение. Полная относительная скорость двух галактик складывается из скорости нх космологического удаления и относительной скорости собственного движения галактик Для далеких галактик космологическая скорость намного превышает собственную скорость галактик (которой в этом случае можно пренебречь), поэтому из наблюдений далеких галактик мы получаем скорость их космологического расширения. Для близких галактик их собстзенная скорость сравнима со скоростью космологического расширения н может даже превышать ее. Поэтому полная скорость может сильно отличаться от космологической и может быгь даже отрицательной. Так, на пример, Туманность Андромеды имеет отрицательную скорость, т. е. она не удаляется от нашей Галактики, а приближается к ней.
Поскольку в настоящее время Вселенная расширяется, расстояние между галакжиками увеличивается, то ясно, что в прошлом они были расположены ближе друг к другу и размер наблюдаемой Вселенной (Метагалактики) был меньше. Следовательно, средняя плот ность вещества была выше, т. е. условия во Вселенной в прошлом отличались от тех, которые имею г место в настоящее время. Но насколько велико это различие? Закон Хаббла сам по себе не дает OTBeia на ггот вопрос. Здесь необходима помощь теории Мы должны обратиться к космологическим моделям и выбрать ту из них, которая лучше соответствует наблюдениям.
Простейшей и, как казалось, наилучшим образом соответствующей наблюдениям является модель Фридмана однородной изотропной Вселенной с Л-членом, равным нулю. В этой модели действуют только силы гравитации[91]. Если в некоторый момент остановить расширение Вселенной, то в следующий момент под действием гравитации она начнет сжиматься. Поскольку в настоящее время Вселенная расширяется, значит, когда-то в прошлом, в какой-то начальный момент времени, по причине, о которой мы пока ничего не знаем, частицы вещества приобрели скорость разлета, подобно облаку газа, образовавшемуся при взрыве. В дальнейшем Вселенная расширялась по инерции, а силы тяготения тормозили расширение. Динамика Вселенной зависит от соотношения между началь ной скоростью и силами тяготения, которые определяются средней плотностью вещества во Вселенной. Если плотность не превышает некоторого критического значения (р < рК(1), то силы тяготения
не в состоянии остановить расширение, и Вселенная будет расширяться неограниченно. Если р > рК|„ то силы тяготения останавливают расширение; в некоторый момент постоянно уменьшающаяся скорость расширения обращается в нуль, после чего Вселенная начинает сжиматься.
|
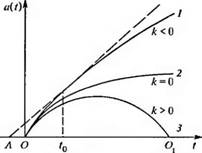
Рис. 2.2.3. Изменение масштабного фактора в модели Фридмаи с Л-члспом, равным нулю По горизонтальной осн oi южено врем" по вертикальной масштабный фактор А(1): I — р < ркр; 2 — р = pKi); 3 — р > рч>. Угол наклона касательном к кривым и любой точке этого графика определяет скорость расширения Вселенной в соответствующий момент времени — современный момент времени. Отрезок /1/0 определяет хаббловскос время I/Нв Для открытой модели (при р< р^) |
На рис. 2.2.3 показано, как изменяется с течением времени масштабный фактор a{t) в рассматриваемой модели Поскольку расстояние между любыми точками в расширяющейся Вселенной пропорционально масштабному сЬактору (R{T) = I0Ci(T)), то аналогичным образом будет меняться расстояние между дзумя любыми далекими галактиками, радиус Метагалактики и, вооб ще, радиус любой достаточно большой сферы, выделенной во Вселенной.
Такой характер изменения масштабного фактора можно попять, исходя из следую. цих соображений. Выделим мысленно в однородной Вселенной некую сферу пронз вольного, но достаточно большого радиуса, так, чтобы в пей содср жалось большое число галактик. Рассмотрим «частицу» вещества (галактику), находящуюся на гра ннце сферы[92]"’. Она обладает он ределепной скоростью, с которой удаляется от центра сферы, и соответствующей кинетической энер гией. Как будет двигаться такая галактика по отношению к центру сферы? В однородной Вселенной на галактику действует только тяготение вещества, расположенного внутри сферы; тяготение наружных слоев взаимно уравновешивается Следовательно, задача аналогична задаче о движении тела, например ракеты, находящейся на поверхности планеты, которой сообщили вертикальную скорость. Полная энергия Е выбранной нами галактики складывается из кинетической н потенциальной, последняя определяется силами тяготения. В процессе расширения Вселенной
кинетическая н потенциалььая энергии изменяются, а лолная энергия Е остается без изменения (закон сохранения энергии) Напомним, что потенциальная энергия отрицательна, а кинетическая энергия — положительна Полная энергия зависит от плотности. При р < рк[1 полная энергия Е > 0; это соответствует случаю, когда ракета приобретает скорость, превышающую вторую космическую. Как известно, в этом случае она будет двигаться по гиперболической орбите, неограниченно удаляясь от планеты, причем скорость на бесконечности будет стремиться к предельному значению Rf > 0. Так же будет вести себя и рассматриваемая нами «пробная» галактика. А поскольку мы выбрали эту галактику совершенно произвольно на поверхности выделенной сферы — так будет вести себя любая другая галактики, зиачит, вся сфера будет неограниченно расширяться. И так как сфера, в свою очередь, выбрана произвольно, то это относится к любой выделенной сфере во Вселенной, т. е. вся Вселенная будет неограниченно расширяться. При р = ркр Е = 0; это соответствует случаю, когда ракета приобретает параболическую скорость Вселенная будет также неограниченно расширяться, только скорость на бесконечности будет стремиться к нулю. Наконец, при р > р полная энергия Е < 0, это соответствует случаю, когда ракета приобр! — тает скорость меньше параболической. В этом случае она удаляется от планеты на определенное расстояние, а затем падает на нее. Подобно этому наша сфера (и любая другая сфера во Вселенной) расширяется до определенного предела, а затем начнет сжиматюг Эта аналогия позволяет понять, почему космологические уравнения без введения дополнительных сил отталкивания не дают статического решения Ведь и ракета не может неподвижно висеть над Землей, она или улетает от нее, или падает на поверхность. Чтобы удержать ракету неподвижно, нужны дополнительные силы.
Критическая плотность, от которой зависит характер расширения Вселенной, определяет также геометрию Мира. При р > ркр мы имеем, как и в модели Эйнштейна, замкнутый мир постоянной положительной кривизны, в котором выполняется геометрия Римана. При р = рК[, Вселенная пространстзеннс бесконечна, кривизна пространства равна нулю, следовательно, в этом случае справедлива евклидова геометрия. Наконец, при р < ркр Вселенная тоже открыта: она бесконечно простирается во все стороны, кривизна ее постоянна и отрицательна; это мир, в котором выполняется геометрия Лобачевского. Таким образом, открытая Вселенная расширяется неограниченно, а в замкнутой Вселенной расширение сменяется сжатием; в момент остановки, ко1да скорость расширения становится равной нулю, радиус кривизны (и объс м) Вселенной достигает максимального значения, а затем начинает уменьшаться.
Какой же сценарий имеет место в действительности? Это зависит от отношения р/ркр. В современную эпоху р =10 29 г/см3. Средняя плотность светящегося (наблюдаемого) вещества, как мы видели, составляет 3 • 10~31 г/см". Эта величина приблизительно в 30 раз меньше критической. Если бы во Вселенной никакого другого вещества не было, мы бы имели вариант открытого бесконечно расширяющегося мира, для которого на больших масштабах справедлива геометрия Лобачевского.
Однако помимо этой наблюдаемой материи во Вселенной существует материя, которая непосредственно не наблюдается, а проявляет себя только • равитационным воздействием. Часть ее может быть обусловлена обычным веществом, сосредоточенном в «коричневых» карликах (о которых мы упоминали в п 2.1.3), но доля его невелика. Считается, что обычное вещество, как наблюдаемое, гак и ненаблюдаемое, составляет не более 5% массы Вселенной (или даже еще меньше), остальные 95% прихс штся на долю так называемой Темной материи или скрытой массы.
Значение этого обстоятельства не всегда оценивается в должной мере. Вдумаемся — все, что мы знаем о Вселенной, основано на изучении не более 5% ее массы! А остальное для нас пока полиостью сокпыто. Чтобы яснее осознагь. что это значит, представим себе, что мы занимаемся реставрацией большого полотна, полностью закрытого позднейшими наслоениями. И вот нам удалось от — рест шрировать 5% картины. Уже проептюют ясно какие-то черты пейзажа. Мы видим деревья на скалистом берегу моря, видим облака на небе, еще какие-то детали. Но мы не можем пока сказать, что представ-тяет собою картина в целом: пейзаж, портрет с пейзажем на заднем или переднем плане, батальная эпопея или бытовая сцена. Примерно в таком же положении оказались астрономы. Дело не в том, чго нам известны не все звезды или не все галактики. Для того чтобы понять строение и эволюцию Вселенной, в этом нет никакой необходимости. Дело в том, что 95% материи — это не I алакгики и не звезды, это не межзвездная пыль и не i аз, это не плазма, состоящая из обычных частиц, из которых строятся атомы вещества. Это нечто, нам пока неизвестное и неизученное. Сказанное не означает, что наши знания о Вселенной не достоверны — нет, го, чго установила наука, достаточно надежно. Но это значит, что наша картина Вселенной на сегодня еще весьма ограничена.
С учетом скрытой массы средняя плотность материи во Вселенной весьма близка к критической Зго означает, что кривизна пространства близка к нулю, мы живем в евклидовом (почти евклидовом) мире.
Какова природа скрытой массы’1 Это тоже до конца неизвестно. Вначале, когда проблема впервые остро встала перед космологией, предполагалось, что скрытая масса может быть обусловлена нейтрино. Долгое время после открытия нейтрино считалось, чго их масса равна нулю. Однако в 1980-х годах экспериментально было обнаружено, что хотя масса нейтрино действительно очень мала, она все же отлична от нуля Первые оценки массы нейтрино давали величину порядка 5-10~зг г, затем они были снижены до Ю-32 г, это в 100 тысяч раз меньше массы электрона, но вполне достаточно, чтобы объяснить всю или почти всю скрытую массу. Действительно, в 1 см4 пространства в современную эпоху содержится около 500 нейтрино всех видов, их общая масса порядка 10"29 г. Однако по современным данным масса нейтрино значительно меньше, и их вклад в массу темной материи невелик. Считается, что подавляющая доля скрытой массы, до 70 %, падает на долю особой «вакуумной материи», равномерно заполняющей всс пространство Вселенной. Эта материя обладает отрицательной гравитацией и является источником тех самых сил отталкивания, связанных с А-членом, которые были введены в модели Эйнштейна (дополнительно см. п. 2 2.3). В отличие от обычной материи, «вакуумная материя» не тормозит расширение Вселенной, а, напротив, ускоряет его. Поэте >му хотя доля этой материи велика, она не может привести к образованию замкнутой Вселенной. Остается еще 30 % скрытой массы. Предпола1 ается, что она может быть обусловлена такими гипотетическими частицами, как аксионы, нейтра — лнно н другие суперснмметричные частицы, которые «с необходимостью» возникают в теории, но экспериментально пока не обнаружены. Иногда в этой связи указывают и на такие тоже гипотетические объекты, как «монополи», «струны», «мембраны», первичные черные дыры и даже горловины «кротовых нор», о которых мы упоминали в § 1.15. Поскольку вклад всех этих объектов точно не известен, рассматривается еще одна возможность — «зеркальное вещество».
Современная физика элементарных частиц принимает в качестве фундаментального постулата симметрию между правым и левым. Отсюда следует, что каждая частица нашего мнра должна иметь свой зеркальный аналог. Из них могут быть образованы зеркальные атомы, молекулы, звезды, галактики и… внеземные цивилизации. При этом час тицы нашего мнра могут взаимодействовать с частицами зеркального мнра только гравитационно. По образному выражению одного нз физиков, через комнату, в которой вы сейчас сидите, может проходить поезд нз зеркальной материи, и никто этого не заметит, если только не будут поставлены тончайшие гравитационные эксперименты. Но по — сколику зеркальное вещество подвержено тяготению, оно вносит свой вклад в скрытую массу нашего мнра (как и наша материя вносит свой вклад в скрытую массу их мира) Если доля обычного вещества (бари — оииая составляющая) в зеркальном мире такая же, как и у нас, зеркальная материя вносит 5% в скрьггую массу нашего мнра. Если барноиная ^оставляющая в зеркальном мире выше, то соответственно повышается и обусловленная зеркальным веществом доля скрытой массы нашего мира. По мнению Н. С Кардашева, доля зеркального вещества может доходить до 25 % ш.
Читателя не должна смущать неопределенность приводимых здесь данных. Обсуждая проблему скрытой массы, мы не только подошли к передовому краю развития науки, но коснулись таких областей, где перед физикой встали фундаментальные проблемы, которые, возможно, существенно изменят чаши представления о мире. Развитие здесь происходит очень быстро, и когда читатель будет пробегать глазами эти строки, многое, наверное, уже изменится.
Важно подчеркнуть, чго хотя мы не знаем точно, какова плотность материи во Вселенной — больше критической или меньше, но она заведомо близка к критической. (Именно потому, что плотность близка к критической, трудно выбрать между двумя альтернативными вариантам!:) Таике надо иметь в виду, что описанный выше характер расширения Вселенной справедлив для модели с Л-чле — ном, равным нулю. Наличие «вакуумной материи» означает, что А-член не равен нулю. Если это так, то истинный характер расширения должен отличат ься от описанного выше.
Каков бы ни был характер расширения Вселенной, в начальный момент (T = 0) масштабный фактор A{T) обращается в нуль (см. рис. 2.2.3). Для замкнутой Вселенной это означает, что ее объем в начальный момент был равен нулю, и значит, она начала расширяться из точки (!). Что касается бесконечной Вселенной, го она всегда остается бесконечной, но любая ее конечная область (в том числе наша Метагалактика) в начальный момент тоже имела нулевой объем. Плотность вещества в этот момент была бесконечной, а скорость расширения стремилась к скорости света. Это состояние бесконечной плотности получило название «сингулярного состояния». Таким образом, в начальный момент Вселенная расширяется из сингулярного состояния с предельно большой скоростью Процесс «возникновения» Вселенной из сингулярности Леметр назвал Большим взрывом.
Какова природа сингу. тярного состояния, реализуется ли оно в действительности? Как близко можно подойти к этому состоянию, изучая историю Вселенной? Что означает «возникновение» Вселенной при T = 0? Что было до этою момента? Эти фундаментальные
ШКардашеь Н. С Кос; юлогпя и цивилизации / Древняя астрономш небо и человек — М., 1998. С. 158-168. Он же. Скрытая масса н поиск внеземных цивилизаций / Препринт ФИАН № 65 — М., 1919 Проблемы космологии не получили пока окончательного решения. Однако за пределами сингулярности теория хорошо согласуется с наблюдениями.
Возникает вопрос — как давно произошел Большой взрыв? Оказывается, можно определю I. этот момент, зная значение постоянной Хаббла"[93]. Если Вселенная расширяется с постоянной скоростью, равной ее современному значению, то время расширения от момента T = 0 до современного момента T0 равно = L/Hv (HL — значение постоянной Хабблт в современную эпоху)133. Это время называется хаббловским временем Фактически время расширения будет отличаться от хаббловского. Для модели с Л-членом, равным нулю, в случае р = рч„ что, как мы видели, близко к действитечьностл:
‘о4—= ||н — (2.4)
0 3 Н0 3 "
Если постоянную Хабб ia Н0 выражать, как это принято в наблюдательной астрономии, в единицах (км/с)/Мпк, а время TH — в годах, то /н = 1012///0. Точное значение Н0 не известно, но из наблюдений следует, что //„заведомо не превышает 100 (км/с)/Мпк, и не меньше, чем 50 (км/с)/ Мпк. Более точная оценка //„: в пределах от 65 до 80 (км/с)/Мпк. Отсюда /„ = 10 + 20 млрд лет, или более точно 12 + 15 млрд лет, а /0= 8 + 10 млрд лет. Здесь опять-таки следует иметь в виду, что и эти оценки справедливы при условии А — 0. В последнее воемя появляется все больше свидетельств того, что А-член не равен нулю и, более того, связанные с ним силы отталкивания приводят к тому, что Вселенная в современную эпоху расширяется Ycnopei но. Если это так, то возраст Вселенной (время от момента T0 до современного момента) должен быть больше хаббловского.
Наличие сингулярности приводит к существованию горизонта Вселенной. Чем дальше от нас находится наблюдаемый обьект, тем ближе к началу расширения Вселенной относится момент времени, когда был испущен свет, достигающий сейчас наблюдателя. Точки в пространстве, от которых до нас доходит свет, испущенный в момент начала расширения (T = 0), и образуют горизонт Вселенной. Горизонт охватывает лишь часть Вселенной, а в случае открытой Вселенной за его пределами находится бесконечное пространство. И тем не менее, ни один объект за горизонтом не может наблюдаться даже с помощью самого совершенного телескопа, ибо за все время существования Вселенной свет, испущенный любым из этих объектов, еще не успел достичь наблюдателя. Эти объекты станут доступными для наблюдения в будущем, когда свет от них дойдет до наблюдателя. Следовательно, горизонт со временем расширяется. В современную эпоху радиус горизонта R = с///,,; в зависимости от значения постоянной Хаббла он составляет 10 • 20 млрд св. лет. На горизонте красное смещение становится бесконечным, а скорость расширения равна скорости света.
|
К |
Сколь близко астрономы подошли к горизонту Вселенной? Если в начале XX века область Метагалактики, для которой были определены расстояния, составляла менее I % от радиуса горизонта, го сейчас она превысила 50 %. Расстояние до далеких объектов (с — > 1) выражается формулой F ч
1—
(2.5)
VT+I,
При к —» оо R(Z) —» Rnlp. Наиболее далекие из обнаруженных к настоящему времени объектов имеют Z порядка 5 + 6. При Z = 6 отношение R(Z)/Rtof = 0,62. Свет, который мы сейчас наблюдаем от этого объекта, был испущен, когда Вселенная была в 18,5 раза моложе и в 7 раз компактнее, чем сейчас. (Здесь мы использовали соотношения: гтГп/Rtlil= I + Z; ‘Mth/’Ifu, = С + *) > справедливые для модели Фрилмаиа при р = р на достаточно поздних стадиях расширения, когда давлением излучения мож но пренебречь.)
Вбли зи горизонта незначительному приращению расстояния соответ ствует большое изменение Z и, следовательно, существенное продвижение в прошлое Вселенной. При этом возможна ситуация, когда из двух объектов более удаленный сейчас в момент излучения находился ближе к нам, чем более близкий (в момент его излучения). Действительно, свет от более удаленного объекта был излучеи давно, когда Вселенная была сильно сжата, и все расстояния в ней, в том числе расстояние от объекта до наблюдателя, были существенно меньше Свет же от более близкого объекта был излучен не так давно, Вселенная была тогда не столь сжата,
и его расстояние от наблюдателя не сильно отличается от современного, поэтому он в момент излучения был дальше от наблюдателя, чем более удаленный объект в момент его излучения. Так в расширяющейся Все ленной проявляется относительность понятий «близкое» и «далекое»: близкое становится далеким и далекое близким.
Проиллюстрируем сказанное следупщим примером. Рассмотрим две галактики с красными смещениями Z, = 2 и Z2 = 5. Используя формулу (2 5), получим ив1 = 1,40. В момент излучения первая галактика
Была в 3 раза ближе к нам. чем сейчас, а вторая — 6 раз ближе Следовательно, расстояние этич галактик в момент излучения было R2Im/Rlnjjl = = 1,40:6×3 = 0,70.
Как долго дчится сингулярное состояние? Длится ли оно бесконечно долго от T = до / = 0, когда Вселенная «вдруг» начинает расширяться, или это короткий, неизмеримо короткий миг? Теория Фридмана не дает ответа на этот вопрос. Более того, теоретики утверждают, что вопрос не имеет смысла, ибо в сингулярности не только не действуют все известные нам физические законы, но и само понятие времени из за квантовых эффектов становится неопределенным. Пусть гак. 11о как бы гам ни было, она как бы возникает из Небытия, проявляется из какого-то непостижимого для нас сингулярного состояния. Этот факт рождения Вселенной при T — 0 и, следовательно, се конечность во времени представляет серьезную проблему в плане философского осмысления Мира.
Если до! 1уст ить, что сингуллрностг дли тся конечное время (с точки зрения «несингулярного» наблюдателя), то, опускал вопрос о том, что творится в самой сиш улярности, правомерно спросить — а что было до сингулярного состояния* Возможно, что ко1да-то, в бесконечно далеком прошлом, Вселенная сжималась из крайне разреженного состояния, плотность ее со временем увеличивалась до тех пор, пока постоянно уменьшающийся масштабный фактор при 1 = 0 Ни обратился в нуль — Вселенная перешла в сингулярное состояние, после чего начала расширяться. Мы живем на стадии расширения, которая в случае открытой модели будет продолжаться бесконечно долго. Этот сценарий снимает трудность с возникновением Вселенной — Вселенная существует вечно (от «минус бесконечности» до «плюс бесконечности»). При этом она один раз проходит через сингулярное сост ояние.
Что происходит в момент, когда Вселенная проходит через сингулярность? А. Д. Сахаров, исходя из законов симметрии, предположил, что ири прохождении через сишулярность все частицы заменяются иа античастицы, все пространственные конфиграции
|
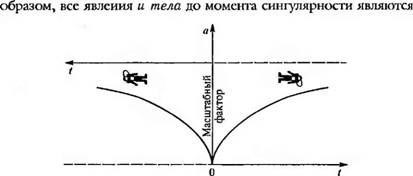
Частиц изменяются на зеркально отраженные, а течение времени меняется на обратное134 (рис. 2.2.4). При этом «сверхкомбинированная», так называемая СРТ-симметрия Мира сохраняется. Таким
Рис. 2.2.4. Гипотетическая модель сжатия Вселснной от состояния бесконечно малой плотности до сингулярности с последующим неограниченным расширением. По вертикальной оси отложен масштабный фактор, по горизонтальной — время. Согласно гипотезе А. Д.Сахарова. при прохождении через сингулярность частицы меняются на античастицы, левое на правое, и ход течения времени меняется иа обратный. Нижняя горизонтальная линия изображает ход течения времени в нашем мире, верхняя — в антимире |
Точной зеркальной копией гел и явлений после этого момента с заменой частиц на античастицы и с заменой направления течения процессов. С нашей точки зрения, Мир до сингулярности (Ан гимир) существовал в далеком прошлом, когда Вселенная еще сжималась. Но с точки зрения обитателей Антимира (не хочется называть их аити — людьми, хотя они состоят из антивещества и имеют сердце с правой стороны) — это наш Мир существует в их далеком прошлом, причем наш Мир, следуя направлению их времени, сжимается, а их Мир — расширяется. «Фактически ОНИ—это МЫ (или МЫ — это ОНИ), так как с точностью до условного определения знака времени, условного отличия правого от левого и условного отличия вещества от аигивещества, отраженный мир не отличается от нашего»[94]®.
В случае замкнутой Вселенной расширение, как мы видели, сменяется сжатием. В конце ст адии сжатия Вселеннтя приходит в сингулярное состояние, такое же, из которого она начала расширяться.
Следовательно, те же силы и те же причины, которые привели к расширению Вселенной в начальный момент времени, теперь снова заставлт ее начать расширяться. В конце нового цикла картина вновь повторится и т. д. Мы получим, таким образом, вечно существующую пульсирующую Вселенную, в которой периоды расширения — сжатия разделены сингулярностями. Если каждый раз в сингулярности происходит замена Мира на Ашимир (как описано выше), то эволюция Вселенной во времени будет представлять собой чередующуюся вереницу миров и антимиров, между которыми Вселенная пребывает в сиш-улярном состоянии. Возможность существования пульсирующей модели Вселенной была ясна еще Фридману. В..вязи с этим он вспоминал сказания индусской мифологии о периодах жизни. Действительно, в индусской мифологии и в древнеиндийской философии существует представление о периодическом процессе проявления (манифес :ации) Вселенной, в котором активные процессы — Манвантары чередуются с пассивными периодами — Пралайями, образуя циклы различного масштаба длительности136. Самый крупный цикл — Махакалыта составляет 311 040 ООО ООО ООО = 3- 10[95] нет. Махакалыта — это Век Брамы, он состоит из 100 Годов Брамы. Каждый Год делится на 360 су. о к (360 Дней и 360 Ночей Брамы). Одни Сутки Брамы равны 8 640 000 00С лет, а одна секунда в этом масштабе времени составляет 100 000 земных лет. Обращает внимание, что Сутки Брамы по порядку величины близки к дли тельности расширения во Фридма — новской Вселенной (8 + 10 млрд. лет). Если принять, что длительность расширения /„ в точности равна Суткам Брамы, то получим постоянную Хаббла Н0 = 77 (км/с)/Мпк, что попадает как раз внутрь интервала неопределенности для Н0: 65 + 80 (км/с)/Мпк.
Привлекательной чертой пульсирующей модели является то, что она позволяет избежать проблемы Генезиса Вселенной. Однако некоторые космологи указывают, что это не так Дело в том, что в каждом цикле Вселенной как в период расширения, так н в период сжатия происходит рост ипропии (которая в конечном итоге определяется числом фотонов, приходящихся на один нуклон). Ьсли накопленная в данном цикле энтропия сохраняется при переходе через сиигуляторность, то в каждом следующем цикле энтропия будет выше, а следовательно, максимальный радиус кривизны (связанный с энтропией) и период пульсации будут больше, чем в предыдущем (рис.2 2 5). То есть будет происходить «раскачка» Вселенной. Необходимая для раскачки положительная энергия берется за счет отрицательной энергии гравитационного поля, а полная энергия, равная сумме положительной и отрицательной энергии, не меняется, т. е. закон сохранения энергии при переходе от цикла к циклу
|
|
Рис. 2.2.5. Изменение масштабного фактора в осцилирующей модели Вселенной а) без увеличения лпропии; б) с увеличением штропии
Выполняется. Если бы пульсирующая Вселенная существовала бесконечно долю в прошлом, то за бесконечное число пульсаций должна была накопиться бесконечная энтропия Но этого нет Следовательно, с момента возникновения Мира прошло конечное число пульсаций, т. е мы снопа возвращаемся к проблеме Начала, только отодвигаем его во времени. Следует отметить, что эти рассуждения справедливы, если энтропия при прохождении через сингулярность сохраняется. Предположение — далеко не очевидное, если учесть, какие глубокие преобразования происходят в сит улярностг.
Мы рассмотрели механическую картину эволюции Вселенной, не касаясь физики процессов. Теперь нам следует обратиться к физике