Мы ис преклоняем главу во прах перед тайной разума, ибо разрешили ее века назад
«Чаша Востока»
В предыдущих параграфах этой главы мы рассмотрели два подхода, которые используются при изучении проблемы КЦ экораполяци — онный и системный В отличие от этого, В. А Лефевр, известный советский психолог и математик, работающий ныне в США, предложил принципиально иной подход. Он вообще не использует «тех нократическое» понятие «цивилизация», а оперирует понятием «Космический субъект». Отличительной особенностью Космического субъекта Лефевр считает наличие совести. «Наша специфическая особенность, — пишет он, — состоит не столько в том, что мы умны, сколько в том, что мы обладаем совестью <…> .. формальная структура совести и является тем специфическим качеством, которое характеризует класс подобных нам космических существ. Такие существа, будучи тождественны нам своими глубокими человеческими переживаниями, могут, тем не менее, быть бесконечно далеки от нас по своей физической природе»[212].
Лефевр развил математическую модель субъекта, совершающе1 о выбор одной из двух полярных противоположностей, например моральный выбор между добром и злом, и способного проводить при этом последовательные акты саморефлексии, самоосознания. Чтобы избежать недоразумений, следует подчеркнуть, что понятия «добро» и «зло» в рамках модели не определяю 1ся. Определение их относится к компетенции философии, религии, этики. Модель лишь описывает поведение субъекта, принимающего ту или иную концепцию добра. Это свойство любой математической модели: она даег общие закономерности поведения системы, а конкретное «физическое содержание» определяется в зависимост и от решаемой задачи. Например, математическая теория колебательных систем описывает их общие закономерности, Но в зависимости от решаемой задачи, она может прилагаться к описанию колебаний физического маятника или электрических осциляторов и т. д.
Точно гак же Космический субъект может придерживаться разной философии, религии, этики, и его конкретные действия, в зависимости от этого, Moiyr различаться, но общие математические
Космический субъект Лсфсвра
Закономерности поведения, связанного с выбором между двумя этическими полюсами и осознанием этого выбора, будут одинаковы. Именно они и описываются моделью. Читателю следует иметь в виду это обстоятельство[213].
5.5.1. Математическая модель Лефевра. Поведение субъекта в модели Лефевра описывается с помощью величины У,. Если субъект всегда выбирает добро, Yx = 1; если субъект всегда выбирает зло, У, н 0. В общем случае субъект с определенной вероятностью выбирает либо добро, либо зло: Y — это вероятность того, что субъект выберет добро, а (1 — У() — вероятность того, что он выберет зло.
Выбор субъекта зависит от трех величин хь х2, х3. Величина х, характеризует давление среды: х{ = 1, если мир диктует субъекту сделать положительный выбор; хх = 0, если мир диктует субъекту сделать отрицательный выбор. В общем случае х, — вероятность того, что мир диктует положительный выбор, 0 <xt < 1. Поведение субъекта определяется не только давлением среды но и его представлением об этом. Величина х2 характеризует представление субьек — та о том, что ему диктует мир. Если субъект думает, что мир диктует ему выбрать добро, х2 = 1; если он думает, что мир диктует ему выбрать зло, х2 = 0. В общем случае х2 — это вероятность того, что субъект думает, будто мир диктует ему выбрать добро, 0 < х2 < 1. Наконец, х3 характеризует желание самого субъекта: х3 = 1, если субъект желает сделать позитивный выбор, и х3 = 0, если он жслает сделать негативный выбор. В общем случае х3 — вероятность того, что субъект хочет сделать позитивный выбор, 0 < х3 < 1. Поведение субъекта есть функция величин хь х2, х3. Это можно записать в виде У[ =/(х1, х2, х3). Чтобы иметь возможность делать конкретные численные прогнозы, надо знать вид функции _Дхь х2, х3).
В модели Лефевра зависимость Y} = F(Xu х2, х3) дастся простым алгебраическим выражением:
У, = х, + (1 — х,-х2 + х, х2) х3; (5.14а)
|
—- 521 |
Или
У, =х,+ (1-х,)(1-х2)х3. (5.146)
Пусть л*! = 0 и л*2 = 0, тогда F, = х3, т. е. поведение субъекта совпадает с его желанием. А это означает, что субъект обладает свободой воли. Правда, свобода воли реализуе гея при единственном наборе значений параметров х1 и х2 (*1 = х2 = 0). Пусть при этом х3 = 0, тогда К| тоже равен нулю, это представляется тривиальным. Гораздо интересней другой крайний случай х3 = 1, У = 1 Значит, если субьект желает выбрать добро, то он выбирает его, несмотря на то, что мир толкает его к противоположному выбору (Х] = 0), и он знает об этом (х2 = 0). Отсюда сисдуег, что если субъскг сделал негат ивный выбор (Y{ = 0), то его внутреннее желание было нсгат явным. То ее ть суб»ект, имеющий свобод)’ воли, несет ответственность за свой выбор.
Вероятность х3, с которой субъект намерен сделать тот или иной выбор, вообще говоря, отличается от вероятности Кь с которой он реально делает этот выбор. Если Yi Ф х3, это значит, что субъект хочет сделать один выбор, а фактически (под влиянием обе тоя — тельств) делает другой выбор, т. е. его желание, его внутренний выбор является нереалистичным Если при некоторых значениях параметров Xi И х2 выбор Yx = х3, то такой выбор можно считать реалистичным. Субъект, для которого выбор всегда (при любьгх значениях параметров и х2) реалистичен, Лефевр называет Реалистом. Для Реалист?..
=—— ——- , еслих|+х2>0. (5 15
Хх + х, — ‘,х2
Следующий шаг связан с введением полезности альтернатив Смысл этого понятия можно уяснить с помощью такого примера. Пусть некто хочет продать свой пистолет. Он может сдать его в полицию и получить 20 долларов, а может продать торговцу оружием и получить 50 долларов. О, [нако в этом случае пистолет может попасть в руки преступника. Сдача пистолета в полицию ассоциируется с позитивным выбором, а продажа торг овцу оружием — с отрицательным. Полезность в данном случае ассоциируется с выгодой, измеряемой ценой пистолета в том или другом случае. Позитивный вьгбор имеет полезность 20, негативный — 50. Математически задача аналогична психологическому эксперименту, когда испытуемому предъявляется набор стержней разной длины, затем набор убирается, демонстрируется один из ранее показанньгх стержней, и испытуемый д( лжен ответить на вопрос, каким является данньгй стержень — длинным или коробим. Здесь полезности определяются в единицах «похожести» на самьгй длинный или самьгй короткий стержень. Но емьгел их тот же.
Космический субъект Лефевра — ————————————- — 523
Обозначим полезное™ позитивного и негативного полюса на нео сознанном уровне V2, а те же полезности па уровне знания иъ и2. Величину X] можно интерпретировать как давление в сторону позитивного выбора на неосознанном уровне, а величину х2 — как давление в сторону позитивного выбора на осознанном уровне (или уров не знания), соответственно (1 — х j) — давление в сторону негативного выбора на неосознанном уровне, а (1 — х2) — давление в сторону негативного выбора на уровне знания. Предполагается, что величина давления пропорциональна нолезностям альтернатив. То есть:
V. V-,
X, = , 1-х, = — ; (5.16)
A, + v2 vy + v2
Х7 — , 1-х,= . (5-17)
If, + и2 ‘ и, + и2
Подставляя эти значения х( и х2 в (5.15), получим:
К, =—— ——— , если у,+гу,>0. (5.18)
V, +- [214]—V,
И, + и2
В задаче о продаже пистолета можно положить у, = м, = 20, V2 = к2 = 50. Следовательно,
20
Y. =———— ——т—— г — 0,583.
20 + 20×50/(20 + 50)
То есть модель предсказывает, что при данных условиях человек сдасг свой пистолет’ в полицию с вероятностью 0,583.
Интересным свойством модели является то, что она позволяет Отделить добро от пользы. Пусть субъект имеет позитивную интенцию (желание выбрать добро), т. е. х3 = 1, н пусть при этом он неукоснительно выбирает добро (У, = 1). Такому выбору соответствует уравнение/(хь х2, 1) = 1, или в развернутом виде:
X,+ (1-х,)(1-х2)1 = 1. (5.19)
Уравнение превращается в тождество при условии xt = 1 или х2 = 0 (или при выполнении одновременно обоих условий). Случай х, = 1 тривиален: субъект желает выбрать добро, мир толкает его к этому выбору, и он делает его. Более интересен случай х, Ф1, х2 = 0. Из (5.17) следует, что это возможно при условии иу = 0, т. е. при условии, когда полезность позитивной альтернативы на уровне знания равна нулю. Иными словами, при положительной интенции и отсутствии «позитивного» диктата мира субъект неукоснительно выбирает позитивный полюс тогда и только тогда, когда на уровне знания позитивный полюс не имеет положительной полезности А это и означает отделение добра от полезности — требование, которое лежит в основе этики всех мировых религий.
5.5.2. Золотое отношение. Модель Лефевра нашла подтверждение в многочисленных психологических тестах, в которых испытуемому предлагалось совершить тот или иной выбор. Она также позволила объяснить ряд психологических феноменов, в том числе результаты голосования на референдумах. Мы не будем останавливаться на этих экспериментах, читатель может познакомиться о ними по книге Лефевра. Рассмотрим в качестве иллюстрации случаи, когда в экспериментах появляется «золотое сечение».
Это относится к ситуациям, когда отсутствуют объективные дан ные для оценки величин. vb х2. Примером может служить экспери мент Р. Зайонца Студентам показывали узоры, напоминающие ки тайские иероглифы. При этом им говорилось, что это настоящие китайские прилагательные и предлагалось оценить степень пози тивности каждого такого «прилагательного». Поскольку узоры на самом деле не были иероглифами, в них не содержится никакой объективной информации о китайских прилагательных. Это пример искусственной ситуации, когда объективная информация о величинах хь х2 отсутст вует. Г1редла1 ались и друг ие эксперименты такого рода. Модель Лефевра в этом случае приводит к уравнению У,2 + У, — 1 = 0. Решение его:
|
|
А это и есть знаменитое «золотое сечение» или «золотое отношение»-1 .
Можно было бы ожидать, что в отсутствие объективной информации о величинах хь л*2 субъект сделает выбор каждой из двух возможностей (0 или 1) с вероятностью, равной 1/2. Но модель в согласии с экспериментом показывает, что это не так: субъект делает асимметричный выбор. Одна из альтернатив выбирается с вероятностью 0,618, другая — с вероятностью 1 -0,618 = 0,372. Число 0,62, как устойчивое значение частоты выбора, появлялось в ряде психологических экспериментов. Однако почему это гак, оставалось не ясным. Некоторые авторы догадывались и выдвигали гипотезу, что точное значение частоты должно равняться золотому отношению 0,618…. Модель Лефевра доказывает это теоретически
Примером более сложной ситуации, когда гакже появляется «золотое отношение», является «задача о разрезании ггирога». Представим себе, что имеется пирог прямоугольной формы. Субъект должен разрезать его на две (равньге или неравные) части и одну из них взять себе. Предполаг ается, что желание взять ту или иную часть пирога пропорционально ее длине. А социальный статус, напротив, обратно пропорционален длине взятого куска: чем больший кусок субъект забирает себе, тем хуже он будет выглядеть в глазах окружающих. И, напротив, чем больший кусок он оставит друг им, тем вьгше его буцуг оценивать. Требуется определить, с какой вероятностью субъект возьмет себе меньшую (или большую) часть. Оказывается модель позволяет не только решить эту задачу, но даст еще дополнительные сведения о том, на какие именно час ги будет раз резан пирог. Модель дает два решения. Первое достаточно одиозное: субъект забирает себе весь пирог с вероятностью 1. Второе решение более интересное: субъект разрезает ггирог в отношении «золотого сечения» 0,618 и берет себе большую часть с вероя тностью 0,618.
5.5-3. Саморефлексирующий субъект. Основная трудность в изучении психологии субъекта, как подчеркивает Лефевр, состоит в том, что его внутренний, q бъективньгй мир полностью недоступен наблюдателю. Единственное, что можно наблюдать — это поведение субиегла которое зависит как от его внутреннего состояния, так и от влияния окружающего мира. Можно ли на основе поведения субъекта судить о его внутреннем состоянии? Путь к этому лежит через изучение процесса саморефлексии, т. е. осознания субъектом своего поведения. Что значит, что субъект осознает свое поведение? Пусть готовность субъекта сделать позитивный вьгбор равна
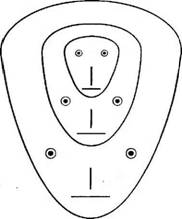
У,; субъект, сознающий свое поведение, не просто готов сделать этот выбор, но он знает, что он готов сделать его. А раз это так, значит субъект имеет некий обрат себя. Причем этот образ, в каком-то смысле, должен быть правильным. Ведь если субъект имеет неправильный образ себя, то трудно говорить о том, что он осознает свое поведение. В процессе последовательной рефлексии образ себя также осознает свое поведение Следовательно, у него появляется свои образ себя. Этот вторичный обр 13 себя Лефевр называет моделью себя (см. рис. 5 5.1). Задача состоит в том, чтобы на основе поведения субъекта извлечь информацию о его Biiyi рением мире или, как говорит Лефевр, о ег о ментальной сфере Согласно Лефевру, это можно сделать посредством математического ана лиза функции, описывающей поведение субъекта.
Как уже говорилось, поведение субъекта определяется давлением внепг него мира лд и взглядом Самого субъекта па свое поведение, его пред ставлением себя или его образом себя Это утверждение можно записать в виде
К, = F(x,,Y2), (5.20)
Где Y2 — образ себя у субъекта. Для того чтобы этот образ был правильным, надо, чтобы переменная У2 выражалась той же самой функцией F, Что и переменная Yj. То есть.
Y2 = F(x2,xy), (5.21)
Где 2 — представление субъекта о воздействии мира, а х3 — представление себя, но не у самого субъекта, а у его образа себя, т. е. это модель себя. Подставляя это выражение тля У2 в (5.20), получим:
К, = F(X„F(X2,.V,)). (5.22)
Но
|
Рис. 5.5.1. Схема саморесЬлекснрую — щею субъекта, по В А Лефевру. Большая рожица символизирует субъект, меньшая, вложенная в нее, — образ себя у субъекта, самая маленькая — модель себя ) губъекта |
К, = х, + (1 — А", — .v2 + л-,л-2)л-3. (5 14а)
Следовательно, мы получаем функциональное уравнение
F{Xu F(X2, Хя)) = л", + (1 — л", — х2 + Щх2)щ (5.23)
Как показал Лефевр, единственным решением этого уравнения явля ется функция
К2 = 1-х3 + х2х3, (5.24)
Которая и описывает образ себя у субъекта Для Реалиста это выражение приобретает вид
Y2 =——— ———— , если л,+дг2>0. (5.25)
Важную роль в модели Лефевра играют диаграммы рефлексии. Для субъекта, совершившего один акт осознания, диаграмма может быть прел ставлена в виде следующей таблицы (матрицы):
|
У1 |
У 1 г, |
|
|
S2 s3 |
(5 26) |
|
|
А", |
Х2 Л*1 |
Здесь. S, — субъект, S2 — образ себя у субъекта, — модель себя.
Диаграмму (5.26) можно прочесть следующим образом. Первый стол бец: мир давит на субъекта St с силой л:, и вызывает реакцию К, (или: стимул А’] действует на и вызывает реакцию К[). Второй столбец: субъект знает, что стимул л’2 действует на него (S2) и вызывает реакцию У2. Третий столбец субъект осознает; что сгимуп х, действует на него (53), вызывая реакцию К,.
В процессе последовательных актов самоосознания субъект переходит из одного состояния в другое. При этом сущность осознания, согласно Лефевру, состоит в том, что предшествующее состояние начинает играть роль модели себя в новом состоянии Для субьекта, совершившего п актов осознания, диаграмма рефлексии имеет вид
Уу Уг Yl… У2 У,
Sj S2 S3 … S,„_, S„, (5.2 7)
X X2 A*[ •■■ X2 Л*1
Здесь M = 2/7+1 и для любой тройки значений Sk_{, Sk, Sk+L. Символ S)| означает образ себя у субъекта Sk_Ly a Sk+L — образ себя у Щ или модель себя у Sk_{.